jag2016-domestic.contest.atcoder.jp
本番バグらせて解けなかった悲しいね.
問題文
省略
解法(反転して表示)
基本的な方針はDPと場合分け.累積和とかである区間の値の総和がO(1)で求めれるように前処理しとく. マスは全て非負なので,空き空間は特に作って得することがないことにまあ気づく.
なので,N=1のときは,与えられた長方形全ての総和が答え.
N=2のときは,垂直もしくは水平な直線でぶった切ってみて,その2つの総和の最小値が答え.
N=3のとき,構成される長方形群はどう配置しても,必ず垂直もしくは水平に分割できる場所があるので,dp[着目長方形の左上][左下][あと何個の長方形を取り出さなければいけないかk]という大雑把な見積もりではO(k(WH)2)な状態数を扱うDPで解ける.遷移は「垂直・水平の分割位置」と「分かれた上下(or左右)の長方形にkをどう割り振るか」を全て試す.
実際の状態数は4乗にはならない.垂直もしくは水平にぶった切るごとに端としてとりうる値の自由度が増えていくのだけれど,一回分割するごとに自由度が1つ増えるだけなので,N<=3なら自由度が高々2なので,大体二乗のdpになっているはず.
問題は,N=4のケースだが,これは,水平or垂直にぶった切れる場所が1つでもあれば,N=3の時のDPと同様にすれば,状態数O(k(WWH+WHH)),遷移O(W+H)のdpで解ける.
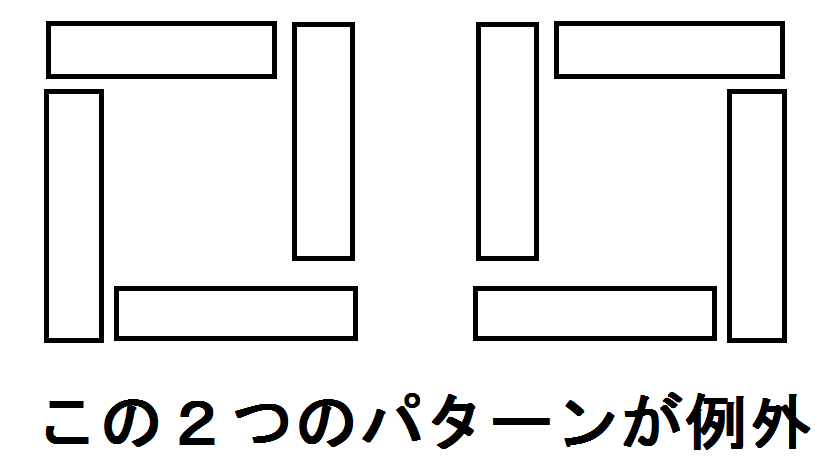
しかし,ぶった切れないときがある.どういうケースかというと,以下のようなケースである.これさえ対策すれば良い.
僕は「下限値の二分探索」+「左上の長方形の形を決め打ちすると連鎖的に他の3つの長方形の形が貪欲で定まる」みたいな感じでこのケースの最適値を求めた.人によっては二分探索使ってない人もいるらしい.
しかも,時計回りのケースを回転・反転したものに対して適用することで反時計回りの法の実装の手を抜いた.
まとめると,N<=3ならDPするだけ,N>=4なら上記の特殊ケースを試してみて大きいほうを返す. 実際の実装ではN!=4でなくともN=4と仮定して特殊ケースを試したり,W=H=200と拡張している.
ソース
#include <bits/stdc++.h>
using namespace std;
map< array<int,4>,int> memo[5];
int A[210][210];
int B[210][210];
int sum[210][210];
int H,W,N;
inline int S(int b,int a,int d,int c){
return sum[c][d] + sum[a-1][b-1] - sum[a-1][d] - sum[c][b-1];
}
int f(const int x1,const int x2,const int y1,const int y2,const int n){
if( n == 1 ){
return S(x1,y1,x2,y2);
}
if( memo[n].count({x1,x2,y1,y2}) ) return memo[n][{x1,x2,y1,y2}];
int ans = 0;
for(int i = x1+1 ; i <= x2 ; i++){
int sub = 0;
for(int j = 1 ; j < n ; j++){
sub = max(sub,min(f(x1,i-1,y1,y2,n-j),f(i,x2,y1,y2,j)));
}
ans = max(sub,ans);
}
for(int i = y1+1 ; i <= y2 ; i++){
int sub = 0;
for(int j = 1 ; j < n ; j++){
sub = max(sub,min(f(x1,x2,y1,i-1,n-j),f(x1,x2,i,y2,j)));
}
ans = max(sub,ans);
}
return memo[n][{x1,x2,y1,y2}] = ans;
}
bool check(int lower){
if( lower == 0 ) return true;
for(int h1 = 1 ; h1 < H ; h1++){
for(int w1 = 1 ; w1 < W ; w1++){
if( S(1,1,w1,h1) < lower ) continue;
int h2 = h1;
while( h2 < H and S(w1+1,1,W,h2) < lower ) h2++;
if( S(w1+1,1,W,h2) < lower ) continue;
int w3 = w1;
while( w3 > 1 and S(w3,h2+1,W,H) < lower ) w3--;
if( S(w3,h2+1,W,H) < lower ) continue;
if( S(1,h1+1,w3-1,H) < lower ) continue;
return true;
}
}
return false;
}
int special(){
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
sum[i][j] = A[i][j];
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
sum[i][j] += sum[i-1][j];
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
sum[i][j] += sum[i][j-1];
int l = 0 , r = 1e9;
while( l != r ){
int m = (l+r+1) / 2;
if( check(m) ){
l = m;
}else{
r = m-1;
}
}
return l;
}
int main(){
cin >> H >> W >> N;
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
cin >> A[i][j];
H = W = 200;
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
sum[i][j] = A[i][j];
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
sum[i][j] += sum[i-1][j];
for(int i = 1 ; i <= H ; i++)
for(int j = 1 ; j <= W ; j++)
sum[i][j] += sum[i][j-1];
int ans = f(1,W,1,H,N);
// N = 4 の入り組んだケース対策.盤面を回転・反転して同じ手法を試してる.無駄があるかも.
for(int __ = 0 ; __ < 2 ; __++){
for(int _ = 0 ; _ < 4 ; _++){
for(int i = 1 ; i <= H ; i++){
for(int j = 1 ; j <= W ; j++){
B[i][j] = A[j][i];
}
}
for(int i = 1 ; i <= H ; i++){
for(int j = 1 ; j <= W ; j++){
A[i][j] = B[i][j];
}
}
ans = max(special(),ans);
// cout << hoge() << endl;
}
for(int i = 1 ; i <= H ; i++){
for(int j = 1 ; j <= W/2 ; j++){
swap(A[i][j],A[i][W-j+1]);
}
}
}
cout << ans << endl;
}